Weitere Unterabschnitte: Digitaltechnik | Logiksimulatoren | Steuerungstechnik | Datenübertragung | Regelungstechnik | Roboter
Digitaltechnik
Allgemein
GeDV-VL10 Mathematische und technische Grundlagen (Prof. Dr. R. Anderl)
- Stellenwertsystem
- Explizite Angabe der Basis
- Gegenüberstellung von Dezimal- Dual- und Hexadezimaldarstellung
- Digitales Prinzip
- Abbildung von Daten in binärcodierter Darstellung
- Diskretisierung und Digitalisierung einer Temperatur-Zeit Darstellung
- Die ASCII Codierung
- Textdarstellung
Die unberechtigte Nutzung ist nicht gestattet.
Sollte evtl. verwendetes material gegen Copyright-Rechte verstoßen, werde ich dieses Material umgehend aus der Seite entfernen.
Analoges und digitales Messinstrument
Die Welt in der wir leben ist analog
Die Welt, in der wir leben ist analog
Alles ändert sich kontinuierlich, stufenlos:
Die Zeit vergeht gleichmäßig – kontinuierlich. Die Zeit springt nicht wie die Anzeige einer Digitaluhr von Sekunde zu Sekunde. Zwischen den angezeigten Sekunden liegen die Zehntel, Hundertstel, Tausendstel… Sekunden, sie werden nur nicht angezeigt.
Temperaturen ändern sich kontinuierlich. Ein klassisches Thermometer zeigt die Temperatur stufenlos (analog) an. Bei einem digitalen Thermometer springt die Anzeige aber jeweils zum nächsten Zehntel Grad (zur nächsten anzeigbaren Stufe).
Ein blauer Himmel hat unendlich viele verschiedene Blautöne. Ein alter Fotoapparat kann dies auf seinem (analogen) Film ganz gut festhalten. Eine moderne Digitalkamera mit X Megapixeln kennt zwar insgesamt über 16 Millionen Farben (genau: 16.777.216 ), aber erstens sind das nicht alles Blautöne und zweitens sind das nicht unendlich viele.
In der Regel reichen uns diese digitalen Anzeigen: die Zeit in Sekunden, die Temperatur in Zehntel Grad und das Blau des Himmels auf dem Bildschirm, aber sie entsprechen nicht wirklich der Realität.
Früher hat man meist analoge Geräte benutzt:
analoge Uhren, Thermometer, Waagen, Maßbänder, Messbecher, Tonbänder, Plattenspieler, Filmstreifen…
Heute wird alles digitalisiert: Aus unendlich vielen Werten werden endlich viele herausgefiltert (Diskretisierung) und als endliche Zahlen dargestellt (Digitalisierung).
Warum macht man das?
Erst wenn die Daten digitalisiert sind, können sie von (digitalen) Computern weiterverarbeitet werden.
Wenn man nicht aufpasst, kann das aber durchaus zu Problemen führen:
Vor etwa 30 Jahren gab’s die ersten erschwinglichen digitalen Taschenrechner. Im Mathe-Unterricht stellte ich die Aufgabe:
1 : 3 x 3
Jeder weiß, dass "Mal" und "Geteilt" entgegegesetzte Rechenoperationen sind und daher ist
1 : 3 x 3 = 1
Zwei Schüler bekamen auf ihrem Taschenrechner aber das Ergebnis 0,99999999.
digital gerechnet
1 : 3 = 0,33333333
0,33333333 x 3 = 0,99999999
Bei modernen Taschenrechnern passiert das natürlich nicht mehr, da sie intern mit mehr Stellen rechnen als sie anzeigen und das Ergebnis dann aufrunden!
analog - diskret - digital
Pocketwatch

Simulation logischer Schaltungen
Simulation logischer Schaltungen
Daher funktionieren diese Simuationen bei Ihnen leider nicht.
Logikgatter mit einem Eingang:
Boolescher Operator:
auffrischen
NICHT (Inverter)
¬
Ziehe ein Logikgatter zwischen den Eingabe-Schalter und die Ausgabe-LED
| Eingabe | Ausgabe |
|---|---|
| A | Q |
| 0 | |
| 1 |
anzeigen:
Bezeichnungen Wertespalten Wahrheitstabelle Boolescher Operator
Am Inverter ist die verwendete Symbolik gut zu erkennen: Ein kleiner Kreis am Ausgang des Gatters bedeutet, dass der Wert umgekehrt (invertiert) wird.
Anmerkungen:
- Falls sich jemand – zu Recht – fragt, warum die Lampe überhaupt leuchten kann, da doch kein geschlossener Stromkreis vorliegt: Die Schaltung ist so zu verstehen, wie es
früher z.B. bei Fahrrädern üblich war. Stromquelle und Lampen waren mit dem Fahrradrahmen
(Eisen) verbunden und dieser schloss den Stromkreis. Auch hier muss man sich eine zusätzliche – unsichtbare – Verbindung aller Bauteile vorstellen, die nur zur Vereinfachung weggelassen wurde! - Aber wie kann dann die Lampe leuchten, wenn alle Schalter aus sind? Der Strom vom Schalter dient nur zur Steuerung des Gatters. Jedes Gatter besitzt eine eigene – hier auch unsichtbare – Stromversorgung (Sekundärkreis) über die die Lampe gespeist wird!
Logikgatter mit zwei (oder mehr) Eingängen:
Boolesche Operatoren:
ODER
V
Nicht ODER
UND
Λ
Nicht UND
Exklusives ODER
V
Ziehe ein Logikgatter zwischen die Eingabe-Schalter und die Ausgabe-LED
| Eingabe | Ausgabe | |
|---|---|---|
| A | B | Q |
| 0 | 0 | |
| 0 | 1 | |
| 1 | 0 | |
| 1 | 1 | |
anzeigen:
Bezeichnungen Wertespalten Wahrheitstabelle Boolesche Operatoren
Speichern von Daten… lassen sich durch Kombination dieser einfachen Logikschaltungen
aufbauen.Tatsächlich genügen sogar nur NOR-Gatter oder nur NAND-Gatter zum Aufbau
beliebiger digitaler Schaltungen.
Logiksimulation am PC mit Hardwareanbindung
The Logic Lab: simulating simple circuits of logic gates

Digitaltechnik
analog-digital
Daher funktionieren die Eigabeschalter und Ausgabeanzeigen bei Ihnen leider nicht.
Mit dem Computer kann man Prozesse steuern und regeln
oder dies als Simulation am Bildschirm ablaufen lassen. Für eine solche Prozesssteuerung braucht das Computerprogramm Eingabedaten (Zahlen/Messwerte)Man kann immer nur eine bestimmte (endliche) Anzahl von Zahlen/Werten eingeben.
Mit einem einfachen Schalter ist das leicht. Er hat nur zwei Stellungen:
aus – an (Werte: 0 – 1)
- Schalter
- Lampe
- Wert
- 0
Bei anderen Eingaben ist das komplizierter:
Z.B. ändert sich die Temperatur nicht sprunghaft sondern kontinuierlich (fortlaufend). Wenn die Temperatur von 18°C auf 19°C steigt, dann nimmt sie dabei schon unendlich viele verschiedene Zwischenwerte an.
Wenn man die Genauigkeit der Werte aber beschränkt, dann verschwindet das Problem:
Wenn es nur auf Zehntel Grad ankommt, dann liegen zwischen 18°C und 19°C
nur noch 9 diskrete (diskret = unterschieden, getrennt) Zwischenwerte: 18,1 18,2 … 18,9.
Eine solche Beschränkung auf endlich viele Werte nennt man Diskretisierung. Mit der gleichzeitigen Einschränkung der Genauigkeit der Werte – wie in dem Beispiel – auf eine endliche Anzahl von Dezimalstellen erhält man eine Digitalisierung (digit = Finger, Ziffer).
Analoge Werte (analog = entsprechend) entsprechen der Wirklichkeit. Digitale Werte sind zwar lückenhaft und ungenau, ermöglichen aber die Weiterverarbeitung mit einem (digitalen) Computer.
Wenn man etwas eingeben will, das keine Zahl ist, dann muss man diesem eine Zahl zuordnen:
- Text->Buchstaben->ASCII-Code
- Ton->Tonhöhe/Lautstärke
- Farbe->RGB-Werte
…soll zu gegebener Zeit genauer ausgeführt werden…
Light-emitting diode (LED)
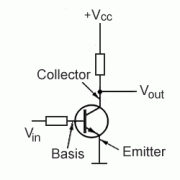
Transistor als Schalter
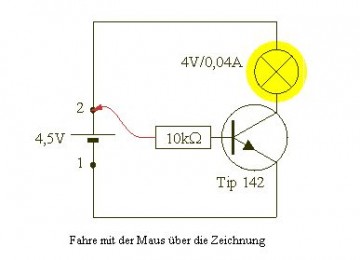
Netzmafia: Prof. Jürgen Plate
- Funktionsweise eines Transistors
- Funktionsweise eines Transistors
Logik-Gatter mit LEGO
GeDV-VL10 Mathematische und technische Grundlagen (Prof. Dr. R. Anderl)
- Boolesche Algebra
- Wertetabelle: Boolesche Funktionen
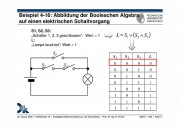
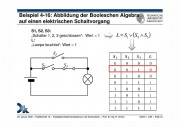
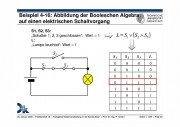
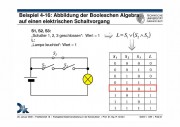
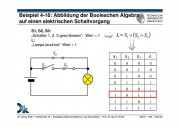
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Abbildung der Booleschen Algebra auf einen elektrischen Schaltvorgang
- Symbole für Verknüpfungsglieder
Die unberechtigte Nutzung ist nicht gestattet.
Sollte evtl. verwendetes material gegen Copyright-Rechte verstoßen, werde ich dieses Material umgehend aus der Seite entfernen.